III.6 Gilpins model and transition Chaos
III.6.1 Extending Lotka-Volterra
Until now every system studied exhibited, in the steady state, one of the 3 types of behaviour:
[1] Continuous steady state: After a long time, every variable in the system assumes a constant value.
[2] Periodic steady state: After all the transients have died out, some variables oscillate with a fixed frequency, while others may assume constant values.
[3] No steady state: The transients never die out; on the contrary, they grow beyond all bounds, that is, the system is unstable.
An interesting question is whether these are indeed all the possible types of behaviour that an (autonomous) system can exhibit. Would it not be feasible that the transients in a system do not die out and yet stay bounded? This question is examined by means of a three-species population dynamics model. The following set of equations describes one predator ![[Graphics:Images/nb3_gr_156.gif]](Images/nb3_gr_156.gif) foraying on two different preys foraying on two different preys ![[Graphics:Images/nb3_gr_157.gif]](Images/nb3_gr_157.gif) and and ![[Graphics:Images/nb3_gr_158.gif]](Images/nb3_gr_158.gif) . The preys suffer furthermore from crowding and competition: This results in Gilpins model (Michael Gilpin: "Spiral Chaos in a Predator-Prey Model," The american naturalist, 52, pp 273-289 (1979)): . The preys suffer furthermore from crowding and competition: This results in Gilpins model (Michael Gilpin: "Spiral Chaos in a Predator-Prey Model," The american naturalist, 52, pp 273-289 (1979)):
![[Graphics:Images/nb3_gr_159.gif]](Images/nb3_gr_159.gif)
![[Graphics:Images/nb3_gr_160.gif]](Images/nb3_gr_160.gif)
![[Graphics:Images/nb3_gr_161.gif]](Images/nb3_gr_161.gif)
REQUIRED
III.6.1a Explain where the crowding, foraying, birth rates and death rates and competition are modelled in Gilpins model.
We can study Gilpins model numerically as follows:
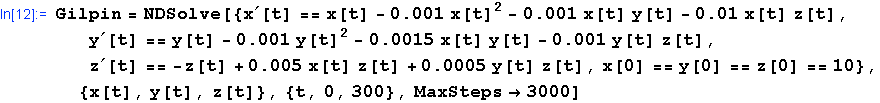
![[Graphics:Images/nb3_gr_163.gif]](Images/nb3_gr_163.gif)
![[Graphics:Images/nb3_gr_164.gif]](Images/nb3_gr_164.gif)
![[Graphics:Images/nb3_gr_165.gif]](Images/nb3_gr_165.gif)
REQUIRED
III.6.1b During most of the time plenty of preys of the 'y' type are around, but from time to time the predator population seems to explode. Show this in a plot. Plot also the dependencies z[t]. Study different time slices. Explain the graphs.
If you look in detail you'll see that each cycle seems to be a little different and no periodic pattern seems to evolve. This type of behaviour is called 'chaotic motion': Transient response does not die out, yet remains stable.
The next graphs show the so-called x-y phase plane of the model.
![[Graphics:Images/nb3_gr_166.gif]](Images/nb3_gr_166.gif)
REQUIRED
III.6.1c Do the same for the x-z and y-z phase planes.
An overview of the complete phase plane is obtained by using a 3-D parametric plot:
![[Graphics:Images/nb3_gr_167.gif]](Images/nb3_gr_167.gif)
![[Graphics:Images/nb3_gr_168.gif]](Images/nb3_gr_168.gif)
III.6.2 Advanced Topic: Transition to Chaos and the Logistics Map
The discrete-time version of the logistic equation (see section III.3.1) can be written as:
![[Graphics:Images/nb3_gr_169.gif]](Images/nb3_gr_169.gif)
We can analyse the steady-state behaviour of this equation as a function of a single parameter ![[Graphics:Images/nb3_gr_170.gif]](Images/nb3_gr_170.gif) . .
![[Graphics:Images/nb3_gr_171.gif]](Images/nb3_gr_171.gif) : We observe a stable continuous steady-state point. : We observe a stable continuous steady-state point.
![[Graphics:Images/nb3_gr_172.gif]](Images/nb3_gr_172.gif) : The steady-state point becomes unstable. : The steady-state point becomes unstable.
![[Graphics:Images/nb3_gr_173.gif]](Images/nb3_gr_173.gif) : Two curves intersect in two points. The second intersection is now a stable continuous steady-state solution of the discrete-time logistic equation. At : Two curves intersect in two points. The second intersection is now a stable continuous steady-state solution of the discrete-time logistic equation. At ![[Graphics:Images/nb3_gr_174.gif]](Images/nb3_gr_174.gif) , this solution is identical with the previous one and thus marginally stable. As we leave the vicinity of , this solution is identical with the previous one and thus marginally stable. As we leave the vicinity of ![[Graphics:Images/nb3_gr_175.gif]](Images/nb3_gr_175.gif) , the steady-state point becomes more and more stable. For example, at , the steady-state point becomes more and more stable. For example, at ![[Graphics:Images/nb3_gr_176.gif]](Images/nb3_gr_176.gif) it takes only a few iterations to reach the steady-state point. As we approach it takes only a few iterations to reach the steady-state point. As we approach ![[Graphics:Images/nb3_gr_177.gif]](Images/nb3_gr_177.gif) , this steady-state point again becomes less and less stable. , this steady-state point again becomes less and less stable.
![[Graphics:Images/nb3_gr_178.gif]](Images/nb3_gr_178.gif) : The system is marginally stable. At : The system is marginally stable. At ![[Graphics:Images/nb3_gr_179.gif]](Images/nb3_gr_179.gif) , it takes infinitely many iterations to reach the steady state point. , it takes infinitely many iterations to reach the steady state point.
![[Graphics:Images/nb3_gr_180.gif]](Images/nb3_gr_180.gif) : at : at ![[Graphics:Images/nb3_gr_181.gif]](Images/nb3_gr_181.gif) : A periodic steady-state with period 2 around the intersection of the two curves. As we leave the area of : A periodic steady-state with period 2 around the intersection of the two curves. As we leave the area of ![[Graphics:Images/nb3_gr_182.gif]](Images/nb3_gr_182.gif) in the positive direction, the periodic steady-state becomes more and more stable (it takes fewer and fewer iterations to reach the limit cycle). In the vicinity of in the positive direction, the periodic steady-state becomes more and more stable (it takes fewer and fewer iterations to reach the limit cycle). In the vicinity of ![[Graphics:Images/nb3_gr_183.gif]](Images/nb3_gr_183.gif) the solution becomes marginally stable. Now the limit cycle splits and we obtain a new limit cycle with a period of 4. the solution becomes marginally stable. Now the limit cycle splits and we obtain a new limit cycle with a period of 4.
![[Graphics:Images/nb3_gr_184.gif]](Images/nb3_gr_184.gif) ![[Graphics:Images/nb3_gr_185.gif]](Images/nb3_gr_185.gif) : The intervals between two new bifurcations become smaller and smaller. Each time the period of the steady-state doubles. At : The intervals between two new bifurcations become smaller and smaller. Each time the period of the steady-state doubles. At ![[Graphics:Images/nb3_gr_186.gif]](Images/nb3_gr_186.gif) we observe a period of 8. Then the period becomes infinite. At we observe a period of 8. Then the period becomes infinite. At ![[Graphics:Images/nb3_gr_187.gif]](Images/nb3_gr_187.gif) the signal has become non-periodic, yet stable: We call this a "chaotic steady state". Then at 3.84 something strange happens, we observe another stable limit cycle, with period of 3. At the signal has become non-periodic, yet stable: We call this a "chaotic steady state". Then at 3.84 something strange happens, we observe another stable limit cycle, with period of 3. At ![[Graphics:Images/nb3_gr_188.gif]](Images/nb3_gr_188.gif) we obtain a totally aperiodic behaviour with random values of we obtain a totally aperiodic behaviour with random values of ![[Graphics:Images/nb3_gr_189.gif]](Images/nb3_gr_189.gif) , anywhere between 0.0 and 1.0. Finally at , anywhere between 0.0 and 1.0. Finally at ![[Graphics:Images/nb3_gr_190.gif]](Images/nb3_gr_190.gif) , the equation becomes unstable. , the equation becomes unstable.
The next figure shows the behaviour of the discrete-time logistic equation in a so-called bifurcation map for ![[Graphics:Images/nb3_gr_191.gif]](Images/nb3_gr_191.gif) . .
On the independent axis, the parameter ![[Graphics:Images/nb3_gr_192.gif]](Images/nb3_gr_192.gif) is varied. On the dependent axis, possible steady-state values of is varied. On the dependent axis, possible steady-state values of ![[Graphics:Images/nb3_gr_193.gif]](Images/nb3_gr_193.gif) are shown. The two branches of the map show the upper and lower value of are shown. The two branches of the map show the upper and lower value of ![[Graphics:Images/nb3_gr_194.gif]](Images/nb3_gr_194.gif) in the periodic steady-state. The dark areas are chaotic. in the periodic steady-state. The dark areas are chaotic.
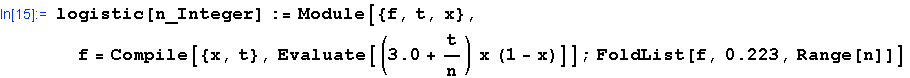
Note that FoldList[f, x, {1, 2, ..,n}] gives {x, f[x, 1], f[f[x, 1], 2], ...}, where t runs through {1, 2, ..,n}. So we end up with ![[Graphics:Images/nb3_gr_196.gif]](Images/nb3_gr_196.gif) with with ![[Graphics:Images/nb3_gr_197.gif]](Images/nb3_gr_197.gif) defined in: defined in: ![[Graphics:Images/nb3_gr_198.gif]](Images/nb3_gr_198.gif) . .
0.223 is chosen as a 'random' initial condition. Examples are given below:
![[Graphics:Images/nb3_gr_199.gif]](Images/nb3_gr_199.gif)
![[Graphics:Images/nb3_gr_200.gif]](Images/nb3_gr_200.gif)
![[Graphics:Images/nb3_gr_201.gif]](Images/nb3_gr_201.gif)
![[Graphics:Images/nb3_gr_202.gif]](Images/nb3_gr_202.gif)
![[Graphics:Images/nb3_gr_203.gif]](Images/nb3_gr_203.gif)
![[Graphics:Images/nb3_gr_204.gif]](Images/nb3_gr_204.gif)
Note that the ![[Graphics:Images/nb3_gr_205.gif]](Images/nb3_gr_205.gif) -axes runs arbitrarily from 1 to -axes runs arbitrarily from 1 to ![[Graphics:Images/nb3_gr_206.gif]](Images/nb3_gr_206.gif) in the plot and is evaluated in logistics as in the plot and is evaluated in logistics as ![[Graphics:Images/nb3_gr_207.gif]](Images/nb3_gr_207.gif) with with ![[Graphics:Images/nb3_gr_208.gif]](Images/nb3_gr_208.gif) E.g: 10000 stands for E.g: 10000 stands for ![[Graphics:Images/nb3_gr_209.gif]](Images/nb3_gr_209.gif) . .
![[Graphics:Images/nb3_gr_210.gif]](Images/nb3_gr_210.gif)
Here we look into the stability around a=1.0, seed 1.0 is chosen to give a scaled plot. If we evaluate for n > 100 we also get scaling problems.
![[Graphics:Images/nb3_gr_211.gif]](Images/nb3_gr_211.gif)
![[Graphics:Images/nb3_gr_212.gif]](Images/nb3_gr_212.gif)
|





