III.1 Fibonacci Growth

Perhaps one of the first mathematical models of a population growth was due to Leonardo Pisano (Fibonacci) in 1202. Let us take a rabbit population model and we will  assume that we have a newborn pair of rabbits that will eventually mate.  We will  assume that rabbits are born in oppositely sexed pairs, which become sexually mature at age 1 month and that the gestational term is 1 month.  

Let denote the number of pairs of rabbits at the end of each month.  Lets look at the different ways we can compute the number of pairs of rabbits at the end of the nth month.

III.1.1 Simple but Inefficient Mathematica Code for the Fibonacci Recurrence

The most natural way to describe the Fibonacci relation in Mathematica is as follows.

REQUIRED  
III.1.1a Derive this function from the described rabbit population.

OPTIONAL
III.1.1b Note that if we want to make a table of Fibonacci numbers, this formula for is horribly inefficient. Explain why.  

REQUIRED
III.1.1c Use the Timing function in Mathematica to measure how long a calculation of Fibonacci series takes for different sizes of the problem. Explain why there is such a difference.

REQUIRED
III.1.1d Using the table command (see "Introduction to Mathamatica")  plot  and fit  the timings.  Any comments?
Hint : look at the function Fit to help you do this.

III.1.2 Improved Code

Mathematica can be convinced to cache its previously computed information about a sequence as follows.
ADVANCED
III.1.2a What do we mean by 'caching the information'? (See "Introduction to Mathematica" for postponed and direct  definitions).

ADVANCED
III.1.2b This approach works good so long as n not too large.  Exaplin  why?.

ADVANCED
III.1.2c Experiment with this approach, and clear Mathematica's memory of the cached values if you run Timing tests so you are not using previously stored information (explain this).

ADVANCED
III.1.2d Compare the timings with the results found in III.1.1

III.1.3 Another Approach

The disadvantage in the above improvement is that in order to compute a Fibonacci number, all the intermediate numbers are stored as rules.  This will  eventually  require a large amount of storage for a term in the sequence if the index is very large.  In fact, for sufficiently large , the process will fail due to exceeded capacity.  Also, the lookup procedure for rules is slow.  These problems can be overcome with an iterative procedure.

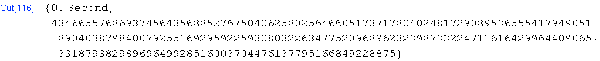
OPTIONAL
III.1.3a Compare your timings with the previous results (plot in one graph for instance)

OPTIONAL
III.1.3b This procedure really flies for the computation of a single value.  It does not have the recursion depth restriction of the previous procedure. Explain this in your own words.

III.1.4 Graphs

To determine the growth rate of the Fibonacci sequence, we can plot the points.

OPTIONAL
III.1.4a Is this exponential?  (To see, you can plot the log of the data and let the data go further out) (These observations are made more precise in the next subsection)

III.1.5 A Closed Form Method

In this subsection, we will derive the standard closed form formula for the Fibonacci sequence to show that the terms  grow exponentially.

The method used to compute F3 can be rewritten in matrix form.

Now the Fibonacci sequence can be described by a matrix equation with appropriate initial conditions (i.e. closed form).

Since the eigenvalues of the matrix A are distinct, the basis can be changed to an eigenbasis (a basis consisting of independent eigenvectors) in order to solve the system. In particular, we can write the start vector X[1] as a linear combination of the eigenvectors of A. If we denote the eigenvalues of A with and and the associated eigenvectors with and respectively, the start vector , where denotes the transposed form of a vector, can be written as

for some and . The pair forms the coordinates of our original start vector with respect to the basis of eigenvectors of A.

Returning to the matrix formulation of the Fibonacci sequence, it is not difficult to see that for an arbitrary

Combining this result with the previous expression for , we find

	=
	=
	=
	=

From the definition of the matrix A the eigenvectors and can be computed. It appears that both are of the form . Substituting this into the expression for gives us

=

This brings us exactly where we want to be. Remember that in the vector the first element denotes the n-th number in the Fibonacci sequence, and the second element the (n-1)-th number. Thus, by concentrating on the first element of the closed form emerges immediately. We only need to know the eigenvalues   and of A, which can easily be determined, and the values for and . These last values easily follow from the equation and the specific form of the eigenvectors. In vector form this equation reduces to

The computation of p and q requires the solution of this linear system.
A formula for can now be determined as follows.

REQUIRED
III.1.5a Determine the complete closed form formula for the n-th term of the Fibonacci sequence given the values for and and the values for and . Describe the behaviour of the Fibonacci sequence for large .

To implement this closed form description as a Mathematica definition is easy.

OPTIONAL
III.1.5b Notice that there is a considerable amount of algebra being done by Mathematica when using this formula to compute large terms in the sequence. Time this function and compare with previously obtained results. Do you have any idea on the differences in memory requirements?

OPTIONAL
III.1.5c In comparing the execution times of the different implementations, you should have discovered large differences. Can you account for the differences by counting the number of operations involved?